OPTAMI: Global Superlinear Convergence of High-order Methods
OPTAMI: Global Superlinear Convergence of High-order Methods
Oct 5, 2024· ,,,,·
0 min read
,,,,·
0 min read
Dmitry Kamzolov
Dmitry Pasechnyuk
Artem Agafonov
Alexander Gasnikov
Martin Takáč
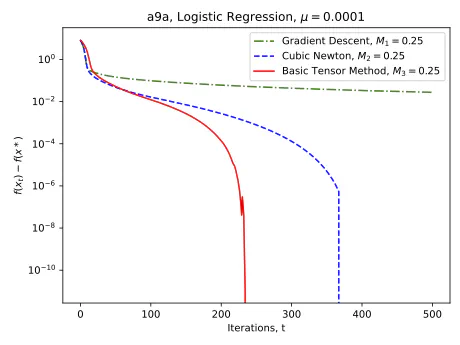 Logistic Regression for a9a dataset from the starting point x0 = 3e, where the regularizer $\mu= 1e−4$ and e is a vector of all ones.
Logistic Regression for a9a dataset from the starting point x0 = 3e, where the regularizer $\mu= 1e−4$ and e is a vector of all ones.Abstract
Second-order methods for convex optimization outperform first-order methods in terms of theoretical iteration convergence, achieving rates up to $O(k^{−5})$ for highly-smooth functions. However, their practical performance and applications are limited due to their multi-level structure and implementation complexity. In this paper, we present new results on high-order optimization methods, supported by their practical performance. First, we show that the basic high-order methods, such as the Cubic Regularized Newton Method, exhibit global superlinear convergence for $μ$-strongly star-convex functions, a class that includes $μ$-strongly convex functions and some non-convex functions. Theoretical convergence results are both inspired and supported by the practical performance of these methods. Secondly, we propose a practical version of the Nesterov Accelerated Tensor method, called NATA. It significantly outperforms the classical variant and other high-order acceleration techniques in practice. The convergence of NATA is also supported by theoretical results. Finally, we introduce an open-source computational library for high-order methods, called OPTAMI. This library includes various methods, acceleration techniques, and subproblem solvers, all implemented as PyTorch optimizers, thereby facilitating the practical application of high-order methods to a wide range of optimization problems. We hope this library will simplify research and practical comparison of methods beyond first-order.
Type
Publication
Preprint, Under Review